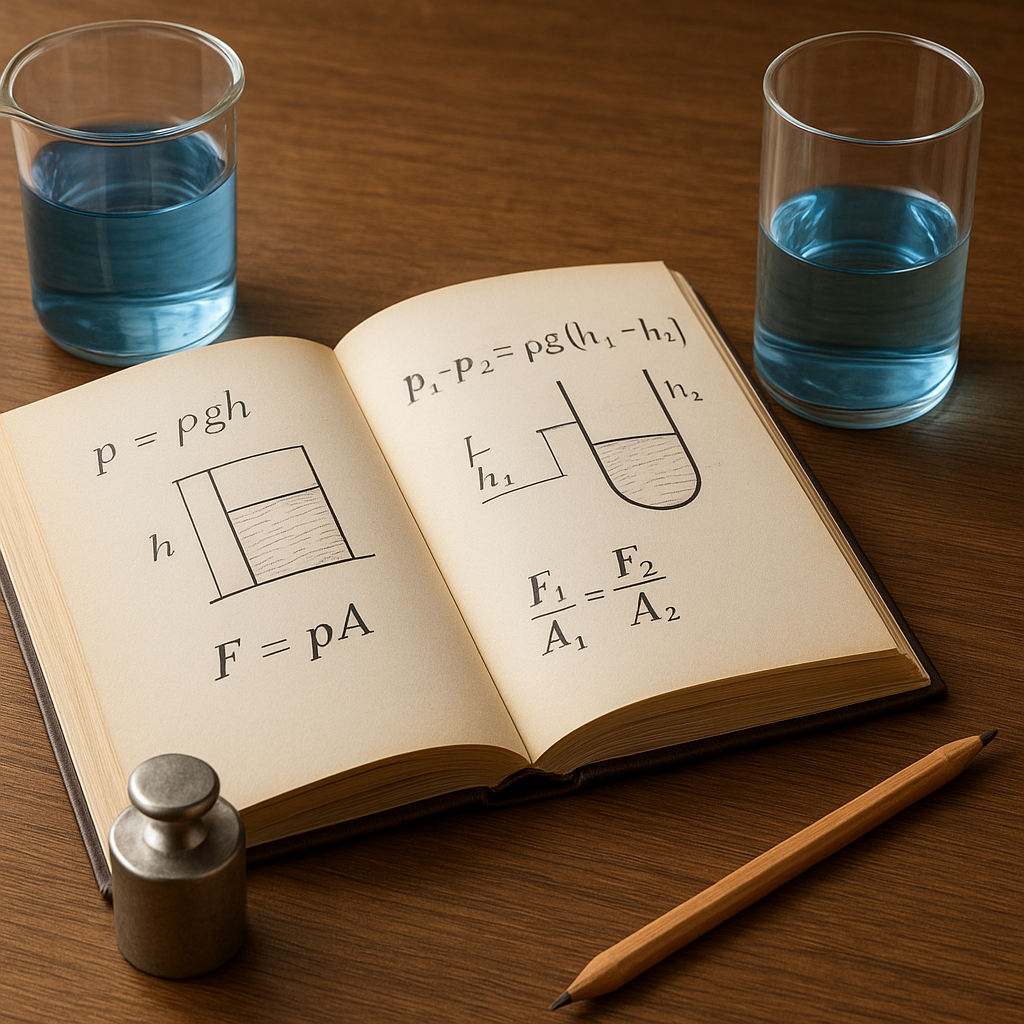Hydrostatyka to dział fizyki zajmujący się badaniem cieczy i gazów w spoczynku. Choć nazwa może brzmieć dość technicznie, jej prawa odczuwamy na co dzień: gdy zanurzamy się w wodzie, obserwujemy unoszące się na powierzchni przedmioty czy zastanawiamy się, dlaczego zapora wodna musi być tak masywna u podstawy. Zrozumienie hydrostatyki pozwala nie tylko lepiej pojmować zjawiska przyrodnicze, lecz także projektować statki, śluzy, zbiorniki wodne, instalacje wodociągowe czy systemy nawadniania. To właśnie w hydrostatyce pojawiają się tak kluczowe pojęcia, jak ciśnienie, gęstość, siła wyporu czy równowaga cieczy. W odróżnieniu od hydrodynamiki, która bada płyny w ruchu, hydrostatyka koncentruje się na sytuacjach statycznych, dzięki czemu stanowi idealny punkt wyjścia do nauki o płynach. W artykule przedstawimy najważniejsze pojęcia, wzory i prawa rządzące zachowaniem płynów w spoczynku, a także przeanalizujemy praktyczne przykłady ich zastosowania. Omówimy, czym jest ciśnienie hydrostatyczne i jak rośnie ono wraz z głębokością, w jaki sposób siła wyporu decyduje o pływalności przedmiotów i jak wykorzystuje się naczynia połączone w technice. Pokażemy też, dlaczego woda w rurach może przenosić nacisk na znaczne odległości, jak obliczać działanie cieczy na ściany zbiorników oraz jak interpretować typowe zadania z fizyki i hydrauliki. Całość będzie ilustrowana opisowymi przykładami, które krok po kroku przeprowadzą przez kolejne etapy obliczeń, tak aby czytelnik mógł nie tylko zapamiętać wzory, lecz także zrozumieć logikę ich stosowania. Dzięki temu hydrostatyka przestanie być zbiorem abstrakcyjnych równań, a stanie się spójnym narzędziem do opisu otaczającego nas świata.
Podstawowe pojęcia hydrostatyki
Hydrostatyka zajmuje się opisem cieczy i gazów znajdujących się w spoczynku. Kluczowe jest tu założenie, że w rozpatrywanym układzie nie występują przepływy ani przyspieszenia, a wszystkie siły działające na płyn równoważą się. Dzięki temu możliwe jest wprowadzenie kilku fundamentalnych wielkości fizycznych, które pojawiają się w niemal każdym zagadnieniu hydrostatycznym.
Jedną z nich jest gęstość, oznaczana zwykle literą ρ. Jest to masa danego płynu przypadająca na jednostkę objętości. Wzór definicyjny ma postać ρ = m/V, gdzie m to masa, a V to objętość. Dla wody w typowych warunkach przyjmuje się gęstość w przybliżeniu równą 1000 kg/m³, podczas gdy dla wielu olejów jest ona mniejsza, co ma konsekwencje dla ich zachowania na powierzchni wody.
Następnym pojęciem jest ciśnienie. W hydrostatyce mówimy o ciśnieniu wywieranym przez płyn na otaczające go powierzchnie. Ciśnienie definiuje się jako stosunek siły działającej prostopadle do danej powierzchni do pola tej powierzchni. Matematycznie zapisuje się to jako p = F/S. Jednostką ciśnienia w układzie SI jest paskal (Pa), równy niutonowi na metr kwadratowy.
Istotną cechą płynów w spoczynku jest ich zdolność do przekazywania ciśnienia we wszystkich kierunkach. W wyniku tego dane ciśnienie w określonym punkcie cieczy działa jednakowo we wszystkich kierunkach, co ma ogromne znaczenie dla konstrukcji urządzeń hydraulicznych i układów technicznych, takich jak prasy czy podnośniki.
Ciśnienie hydrostatyczne i jego wzór
Ciśnienie hydrostatyczne to ciśnienie wywierane przez słup cieczy znajdujący się nad rozpatrywanym punktem. Zjawisko to wynika z działania siły ciężkości na każdą warstwę płynu. Im głębiej znajduje się punkt, tym większy ciężar cieczy nad nim spoczywa, a więc tym większe jest działające tam ciśnienie.
Wzór na ciśnienie hydrostatyczne ma postać p = ρ g h, gdzie ρ to gęstość cieczy, g to przyspieszenie ziemskie, a h to głębokość zanurzenia punktu w cieczy, mierzona od jej swobodnej powierzchni. Warto zauważyć, że w tym uproszczonym ujęciu ciśnienie nie zależy od kształtu naczynia ani od jego rozmiarów, lecz wyłącznie od gęstości cieczy i głębokości. Oznacza to, że w wąskiej rurce i w szerokim zbiorniku, przy tej samej głębokości, ciśnienie hydrostatyczne będzie takie samo.
Istotne jest odróżnienie ciśnienia absolutnego od ciśnienia względnego. W praktyce często mierzy się przyrost ciśnienia w stosunku do ciśnienia atmosferycznego, a więc tzw. ciśnienie nadciśnienia. W zadaniach szkolnych zazwyczaj pomija się wartość ciśnienia atmosferycznego i rozpatruje jedynie ciśnienie związane z zanurzeniem w cieczy.
Prosty przykład: zanurzenie na głębokość 2 metrów w wodzie o gęstości 1000 kg/m³ powoduje powstanie ciśnienia hydrostatycznego równego p = 1000 · 9,81 · 2, co daje w przybliżeniu 19 620 Pa. Zwiększenie głębokości dwukrotnie powoduje proporcjonalny wzrost ciśnienia, co ma istotne znaczenie w budownictwie wodnym i nurkowaniu.
Prawo Pascala i jego zastosowania
Prawo Pascala stanowi fundament działania wielu urządzeń hydraulicznych. Mówi ono, że zmiana ciśnienia wywierana na ciecz (lub gaz) zamkniętą w zbiorniku jest przenoszona bez osłabienia na wszystkie punkty tej cieczy i na ściany naczynia. Oznacza to, że jeśli na jednym końcu układu hydraulicznego wywrzemy dodatkowe ciśnienie, to w całym płynie pojawi się taki sam przyrost ciśnienia.
W praktyce pozwala to na konstruowanie urządzeń, w których niewielka siła przyłożona na małym tłoku może wywołać dużo większą siłę działającą na dużym tłoku, przy zachowaniu równowagi ciśnień. Siła na dużym tłoku jest wprost proporcjonalna do jego pola powierzchni. Tę własność wykorzystuje się w podnośnikach samochodowych, prasach hydraulicznych, hamulcach samochodowych i wielu innych systemach technicznych.
Przykładowo, jeśli w prasie hydraulicznej mały tłok ma pole 2 cm², a duży 40 cm², to stosunek pól wynosi 1:20. Oznacza to, że siła pojawiająca się na dużym tłoku będzie dwudziestokrotnie większa od siły przyłożonej do tłoka małego, przy założeniu braku strat energii i pominięciu tarcia. Tym samym prawo Pascala pokazuje, jak ciecz w spoczynku może służyć do efektywnego przenoszenia i zwielokrotniania sił.
Prawo Archimedesa i siła wyporu
Drugim, równie ważnym prawem hydrostatyki jest prawo Archimedesa, opisujące zjawisko wyporu. Prawo to głosi, że na ciało zanurzone całkowicie lub częściowo w cieczy działa skierowana ku górze siła wyporu równa ciężarowi wypartej cieczy. Jest to rezultat nierównomiernego rozkładu ciśnienia na dolnej i górnej powierzchni ciała zanurzonego.
Wzór na siłę wyporu przyjmuje postać Fw = ρ g V, gdzie ρ to gęstość cieczy, g to przyspieszenie ziemskie, a V to objętość cieczy wyparta przez ciało. Jeśli ciało jest w całości zanurzone, V jest równe objętości ciała. W sytuacji, gdy ciało pływa częściowo zanurzone, objętość wypartej cieczy jest mniejsza i odpowiada tylko tej części objętości, która znajduje się pod powierzchnią.
Siła wyporu stanowi przeciwwagę dla ciężaru ciała. Jeżeli siła wyporu jest większa niż ciężar ciała, obiekt będzie unosił się na powierzchni; jeśli jest mniejsza, ciało zatonie. Warunek równowagi pływającego przedmiotu to równość siły wyporu i ciężaru. Mechanizm ten wyjaśnia, dlaczego duże statki stalowe mogą pływać, mimo że materiał, z którego są wykonane, ma gęstość znacznie większą od wody. Całkowita średnia gęstość statku, uwzględniająca przestrzenie wypełnione powietrzem, jest bowiem mniejsza od gęstości wody.
Równowaga ciał w cieczy
Zrozumienie równowagi ciał zanurzonych w cieczy wymaga porównania wartości siły ciężkości i siły wyporu. W prostym ujęciu można wyróżnić trzy sytuacje. Po pierwsze, jeżeli ciężar ciała jest większy niż siła wyporu, ciało będzie opadać na dno naczynia. Po drugie, gdy ciężar i siła wyporu są sobie równe, ciało osiąga stan równowagi i może pływać częściowo zanurzone lub zawisnąć w cieczy. Po trzecie, jeśli siła wyporu przewyższa ciężar, obiekt będzie wynurzany ku powierzchni, aż do momentu, gdy objętość zanurzonej części zmniejszy się na tyle, by siła wyporu zrównała się z ciężarem.
W praktyce kluczową rolę odgrywa porównanie gęstości ciała i cieczy. Jeśli gęstość ciała jest mniejsza od gęstości cieczy, obiekt z reguły unosi się na powierzchni. Jeżeli jest większa, ciało tonie. Ten prosty warunek jest niezwykle pomocny przy szybkim wnioskowaniu o zachowaniu różnych materiałów w wodzie lub innych płynach. Dzięki temu można projektować konstrukcje o odpowiednim kształcie i wypełnieniu, tak aby osiągnąć pożądaną pływalność.
Naczynia połączone
Naczynia połączone to układ co najmniej dwóch zbiorników zawierających tę samą ciecz, połączonych w taki sposób, że płyn może swobodnie przepływać między nimi. Kluczową właściwością jest tu dążenie cieczy do wyrównania poziomu we wszystkich naczyniach. Wynika to z zasady, że w spoczynku ciśnienie hydrostatyczne na wspólnej wysokości musi być jednakowe we wszystkich punktach.
Jeśli do jednego z naczyń doleje się dodatkową ilość cieczy lub zmieni się jego kształt, poziom cieczy w całym układzie odpowiednio się dostosuje. Zjawisko to jest wykorzystywane w praktyce, na przykład w wodowskazach, układach kanalizacyjnych czy różnego rodzaju instalacjach wodnych. Pozwala ono w prosty sposób kontrolować poziom cieczy w różnych częściach systemu.
Warto zwrócić uwagę, że różne gęstości cieczy w naczyniach połączonych prowadzą do zróżnicowanego ułożenia poziomów. Na przykład, jeśli w jednym z ramion znajduje się woda, a w drugim ciecz o większej gęstości, to aby ciśnienia na poziomie połączenia były równe, wysokości słupów poszczególnych cieczy muszą się odpowiednio różnić. Zjawisko to znajduje zastosowanie w manometrach różnicowych i innych urządzeniach pomiarowych.
Siła parcia cieczy na ściany
Oprócz ciśnienia w konkretnym punkcie często interesuje nas siła, z jaką ciecz działa na daną powierzchnię, na przykład ścianę zbiornika lub tamę. Siłę tę nazywa się parciem hydrostatycznym. Aby ją obliczyć, należy uwzględnić rozkład ciśnienia wzdłuż wysokości powierzchni, ponieważ wraz z głębokością ciśnienie rośnie liniowo.
W najprostszym przypadku pionowej ściany zanurzonej w cieczy przyjmuje się, że ciśnienie zmienia się od zera na powierzchni do maksymalnej wartości na największej głębokości. Średnie ciśnienie na tej ścianie jest wówczas równe połowie ciśnienia maksymalnego. Siłę parcia oblicza się jako iloczyn tego średniego ciśnienia i pola ściany. Względy inżynierskie wymagają, by konstrukcje narażone na działanie dużych słupów wody były odpowiednio wzmocnione w dolnej części, gdzie ciśnienie i parcie są największe.
Takie podejście jest stosowane przy projektowaniu tam, zbiorników retencyjnych i basenów. Zrozumienie, jak rośnie ciśnienie w funkcji głębokości, pozwala nie tylko ocenić wytrzymałość materiałów, ale też prawidłowo rozmieścić zbrojenie i podpory. W praktyce uwzględnia się ponadto zmienne warunki pracy, takie jak zmiana poziomu wody czy wpływ falowania.
Hydrostatyka w przyrodzie i technice
Opisane prawa hydrostatyki mają swoje odzwierciedlenie zarówno w przyrodzie, jak i w rozwiązaniach technicznych. W naturze obserwujemy je w zjawiskach unoszenia się lodu na powierzchni wody, rozkładzie ciśnień w głębokich jeziorach i oceanach czy w różnicy ciśnienia wewnątrz i na zewnątrz organizmów żyjących w głębinach. Dostosowania biologiczne, takie jak pęcherze pławne u ryb, bazują na zmianie objętości gazu i regulowaniu siły wyporu w zależności od głębokości.
W technice hydrostatyka jest nieodłącznym elementem projektowania systemów wodociągowych, kanalizacyjnych, zbiorników, statków, barek i konstrukcji portowych. Urządzenia hydrauliczne, oparte na prawie Pascala, znajdują zastosowanie w dźwigach, hamulcach, układach wspomagania kierownicy czy maszynach przemysłowych. Z kolei zrozumienie prawa Archimedesa jest niezbędne przy projektowaniu jednostek pływających, platform wiertniczych oraz obiektów zanurzonych, które muszą utrzymywać stabilną pływalność.
Przykładowe zadania z hydrostatyki
Wiedza teoretyczna zyskuje na wartości, gdy można ją odnieść do konkretnych obliczeń. Rozważmy kilka typowych zadań, które pojawiają się w kontekście hydrostatyki. Pierwszy przykład dotyczy obliczenia ciśnienia hydrostatycznego na danej głębokości. Zakładając, że mamy wodę o gęstości 1000 kg/m³, można obliczyć ciśnienie na głębokości 5 metrów, podstawiając dane do wzoru p = ρ g h. Otrzymujemy p ≈ 1000 · 9,81 · 5, czyli około 49 050 Pa. Tego typu zadanie wskazuje, jak szybko rośnie ciśnienie wraz ze wzrostem głębokości.
Drugi typowy problem polega na określeniu, czy dane ciało będzie pływać, czy zatonie. Jeśli mamy kostkę o objętości 0,01 m³ i gęstości 500 kg/m³, to jej masa wynosi 5 kg, a ciężar około 49 N. Gdy kostka zostanie zanurzona w wodzie, siła wyporu wyniesie Fw = 1000 · 9,81 · 0,01, czyli 98,1 N. Siła wyporu przewyższa ciężar, więc ciało będzie wynoszone ku powierzchni, aż część kostki znajdzie się nad wodą, zmniejszając objętość wypartej cieczy do momentu osiągnięcia równowagi.
Można także analizować zadania związane z naczyniami połączonymi. Jeśli jeden z ramion układu podniesie się na wysokość h, to w drugim ramieniu poziom cieczy odpowiednio się obniży, przy czym zależność tę można opisać równaniem wynikającym z warunku równości ciśnień na poziomie połączenia. Takie przykłady pomagają zrozumieć, jak zmiany w jednym miejscu systemu wpływają na zachowanie cieczy w innych jego częściach.
Hydrostatyka w praktycznej nauce i edukacji
Dla uczniów i studentów hydrostatyka często jest pierwszym poważniejszym spotkaniem z fizyką płynów. Zrozumienie jej podstaw ułatwia późniejsze opanowanie zagadnień z zakresu hydrodynamiki, mechaniki płynów technicznych oraz inżynierii środowiska. W nauczaniu wykorzystuje się eksperymenty z prostymi naczyniami, rurkami U-kształtnymi, modelami pras hydraulicznych czy zbiornikami z wodą, aby w sposób intuicyjny pokazać, jak zachowują się płyny.
Współcześnie, oprócz tradycyjnych podręczników, coraz większą rolę odgrywają serwisy edukacyjne, które oferują interaktywne materiały, symulacje i przykłady zadań. Jednym z miejsc, w których można znaleźć informacje związane z tym działem fizyki, jest hydrostatyka.pl. Wykorzystanie takich zasobów ułatwia samodzielną naukę, pozwala szybko sprawdzać wzory i trenować rozwiązywanie zadań obliczeniowych, co jest kluczowe dla efektywnego utrwalenia wiedzy.
Znaczenie hydrostatyki w innych dziedzinach
Hydrostatyka nie funkcjonuje w oderwaniu od innych gałęzi wiedzy. Jej prawa wykorzystuje się w geologii przy badaniu ciśnień wód podziemnych, w meteorologii przy analizie ciśnień atmosferycznych oraz w medycynie, chociażby w kontekście pomiaru ciśnienia krwi czy projektowania urządzeń medycznych opartych na cieczach. Inżynierowie środowiska stosują zasady hydrostatyki, by planować systemy retencji wody, zbiorniki przeciwpożarowe, oczyszczalnie ścieków i systemy irygacyjne.
W budownictwie zrozumienie rozkładu ciśnień wywieranych przez wodę na fundamenty, piwnice i podziemne konstrukcje jest konieczne, aby zapewnić odpowiednią szczelność i bezpieczeństwo. W przemyśle chemicznym i spożywczym ważne jest prawidłowe projektowanie zbiorników do przechowywania płynów o różnych gęstościach i właściwościach fizykochemicznych. Wszędzie tam podstawą obliczeń są te same proste wzory hydrostatyczne.
Podsumowanie
Hydrostatyka tworzy spójny i stosunkowo prosty zestaw praw, które jednak mają ogromny zasięg zastosowań. Kluczowe pojęcia, takie jak ciśnienie, gęstość, siła wyporu, równowaga cieczy czy zasada działania naczyń połączonych, pozwalają wyjaśnić zarówno codzienne obserwacje, jak i złożone konstrukcje techniczne. Prawo Pascala umożliwia przenoszenie i wzmacnianie sił w urządzeniach hydraulicznych, natomiast prawo Archimedesa tłumaczy pływalność ciał i stanowi podstawę projektowania jednostek pływających.
Opanowanie podstaw hydrostatyki obejmuje zrozumienie zależności między ciśnieniem a głębokością, umiejętność obliczania siły wyporu i parcia cieczy na ściany oraz świadome korzystanie z pojęcia gęstości. Dzięki temu możliwe jest zarówno rozwiązywanie typowych zadań obliczeniowych, jak i interpretowanie zjawisk przyrodniczych oraz pracy urządzeń technicznych. Wiedza ta jest niezbędna w wielu dziedzinach inżynierii, nauk przyrodniczych i praktyki zawodowej, a jednocześnie pozostaje przekazywana w formie przystępnych wzorów i prostych eksperymentów, które każdy może odtworzyć samodzielnie.